Before continuing the development of the theory, the concept of units and how they transform is discussed. Local observers are observers who make a measurement at a time and location as if they were at that location and time. In forming their measurements, they use units that are both natural and derived. For example, the unit time is derived naturally from a natural oscillation in nature. Then length is derived naturally from the universal speed of light. Derived units come from a combination of base units such as velocity, which is derived from two natural units. A generic list of often used measurements is in The Table below:
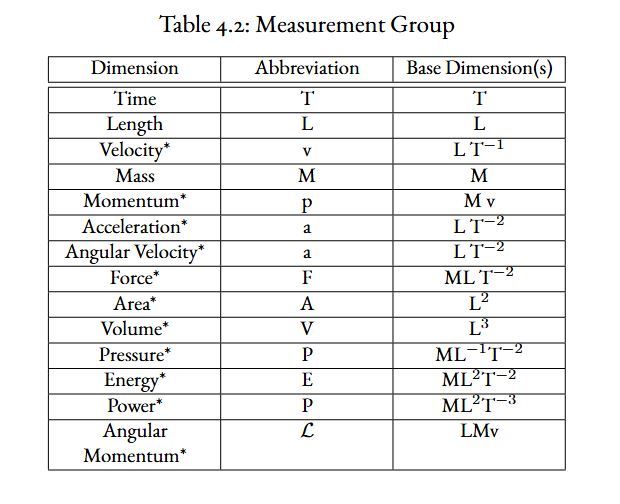
The * marked values are derived values, made up of a combination of natural measurements.
Equipped with length, time, mass, and derived values, one may transform from \(\mathcal{P}\) to \(\mathcal{E}\) or vice-versa using the inverse of \(\phi\). Of note, some derived values transform one to one (they are observed locally the same in both \(\mathcal{P}\) to \(\mathcal{E}\) ). For example, velocity is a derived unit from length and time as follows:
\begin{equation}
v = \frac{Length}{Time}
\end{equation}
Using the NUVO transformation the velocity from \(\mathcal{E}\) to \(\mathcal{P}\) transforms as:
\begin{equation}
v_{\mathcal{P}}= \frac{L_{P}}{T_{P}} = \frac{\phi L_{E}}{\phi T_{E}} = v_{\mathcal{E}}
\end{equation}
Both observers view each other’s velocity as the same, or more precisely, the ratio is invariant in the transformation. Yet acceleration transforms as:
\begin{equation}
a_{\mathcal{P}}= \frac{L_{P}}{T_{P}^2} = \frac{\phi L_{E}}{\phi^2 T_{E}^2} = \phi^{-1}a_{\mathcal{E}}
\end{equation}
Thus, the ratios of units making up acceleration are not invariant under transformation.
Table above shows many familiar derived units and how they transform from \(\mathcal{P}\) to \(\mathcal{E}\).
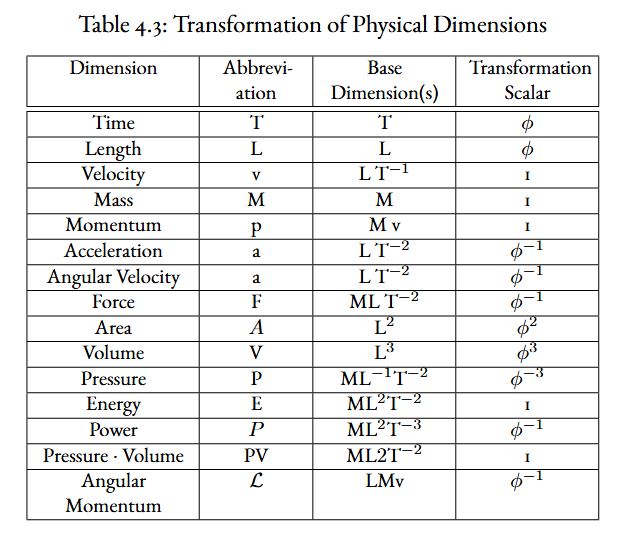
This collection of measuring units can be formed into a group \(\mathcal{G}\) that all observers use in making their observations.
Group \(\mathcal{G}\)
Group of all measuring units, natural or derived, regardless of their transformation \(\phi\) value.
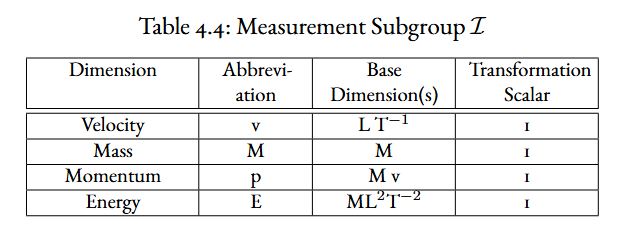
Group \(\mathcal{G}\) can then be divided into two subgroups. One group \(\mathcal{I}\) (for invariant) whose transformation scalar value is 1.
Group \(\mathcal{I}\)
Transformation value for \(\phi\) equals 1.
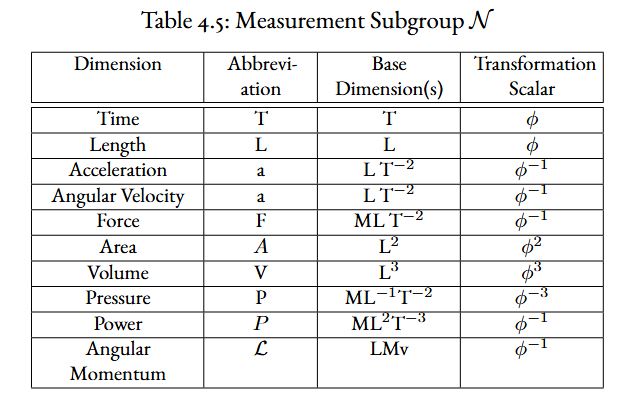
The other group \(\mathcal{N}\) (for not invariant) whose transformation scalar value is not equal to one.
Group \(\mathcal{N}\)
The transformation value for \(\phi\) does not equal 1.
Subgroup \(\mathcal{I}\) and subgroup \(\mathcal{N}\) shown in the tables below. These groups play a role in what the theory predicts as invariant to all observers, and what is invariant under special circumstances.