The above short list of definitions of Riemannian Geometry aims to provide the needed ingredients to help understand the complexity of geometry. It will also serve as a standard to recognize where Einstein “bent” the rules to apply them to his theory. It is challenging to approach a rich subject such as Riemannian Geometry without committing chapters of introduction. The desire here is not to explain or teach geometry; plenty of material exists for that purpose. The goal is to give enough framework of definitions so one can easily understand when they have been violated. What the definitions do not provide a person with are the consequences of violating them. Often, these types of consequences are not known at the time of the violation.
Geometry may be compared to engineering in that both use known and proven concepts to build new concepts (like Euclid’s book, which builds upon each concept). The entire structure, be it a physical bridge or a logical bridge in geometry, depends on the integrity of the components used in engineering. One reason it is often well into the future before a consequence of a violation of integrity is unknown is that the area of violation lays dormant, unused, and unexploited until a future date. It will be shown that there is a direct relation between the unsolved mysteries of General Relativity and the violations of Riemannian Geometry. Only when physicists and mathematicians exploit these areas do they find these mysteries and their inability to observe them physically. Thus, these definitions will play a role later in the book to highlight such areas. NUVO theory strives not to embrace Riemannian Geometry because of its current inadequacy in representing the physical world without violating its tenets.
An area of Riemannian Geometry that is often used is the geodesic. Engineers often use this function to find the optimized path for a roadway over a mountain. Geodesics are also used to find the shortest path for a flight from one location on Earth to another. Though the Earth is not a perfect sphere, it is close enough that treating the Earth as a sphere provides highly optimized geodesics for travel. In General Relativity, Einstein uses geodesics to find the path of a free particle (a particle with no external forces applied). These geodesics provide the familiar mappings of a gravity well that is popular when demonstrating General Relativity. See Figure 2.3.
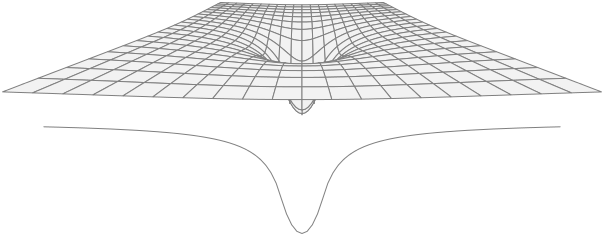
Outside of physics, Riemannian geometry and the application of manifolds may be observed in disciplines such as finance, medicine, artificial intelligence, and most anywhere the need to study a surface area is found. Riemannian geometry is still being studied and applied across many disciplines with splendid success.