Antigravity Particle Simulation
See simulation below. Work in progress.
1. Introduction
Antigravity’s definition is more of a concept than a firm definition since no antigravity experiment has successfully shown any results to support a definitive definition. Thus, for the purpose of this paper a definition is provided for antigravity particles and antigravity particle effects. The antigravity particle is in close relation to negative mass as described by H. Bondi [1].
1.1 Antigravity Particle
An antigravity particle is a particle that
- Attracts other antigravity particles
- Repels gravitational particles
1.2 Antigravity Particle Effects
- Generates an inverse gravitation well in the curvature of space-time
- Curves a light wave away from the particle.
Using these definitions, a simulated scenario of interacting gravitational particles and antigravity particles is constructed. Once constructed, the simulation iterates through a series of steps applying the effects to the system of particles.
2 The Model
2.1 Using Classical Based Derived Equations to Calculate the Force Between Particles
In Newtonian gravity the force between two masses is.
\(\begin{equation}\tag{1}
F= -\frac{G M m}{r^2}
\end{equation}
\)
Newton’s equation is modified slightly in the classical based approach to General Relativity by multiplying the force by a scalar value representing the time and length dilation (curved space) due to the presence of a massive object.
\(\begin{equation}\tag{2}
F= A \frac{G M m}{r^2}
\end{equation}
\)
Where A is the scalar dilation, read Gravitational Time Dilation Derived from Special
Relativity and Newtonian Gravitational Potential [2] for a full derivation of the scalar value.
\(\begin{equation}\tag{3}
A= 1 + \frac{T-V}{E_0}
\end{equation}
\)
Where T is the kinetic energy of the particle, V is the potential energy of the particle, and E0 is the rest energy of the mass generating the gravitational effect. The particles mass in the simulation is of a small enough magnitude the A value has little effect, but is included for completeness.
The same force equation is used to calculate the force between antigravity particles. The force between an antigravity particle and a gravitational particle will use Equation (1) except the force is repulsive (positive). The interaction between the particles is shown in Figure 1, where the red Anti particles are antigravity particles and the blue Norm particles are gravitational particles.

2.2 Initial Conditions
The initial conditions for the simulation are setup by randomly placing 2500 antigravity particles and 2500 gravitational particles within a cubic volume (200 cubic units). The particles have zero velocity initially. Each particle has the same magnitude of mass.
The particles have a spherical radius of 1 unit. If the particle’s location is within radial distance of another particle’s center (and they are the same type of particle), they are merged. The merged particle radius grows by ten percent per merger and acquires the sum of momentum and mass of the merged particles. A visualization of the initial conditions of the particles can be viewed in Figure 2.

3. Simulation
If the antigravity particles were invisible (or the gravitational particles were invisible, but observed effects by the antigravity particles), it provides a different perspective.
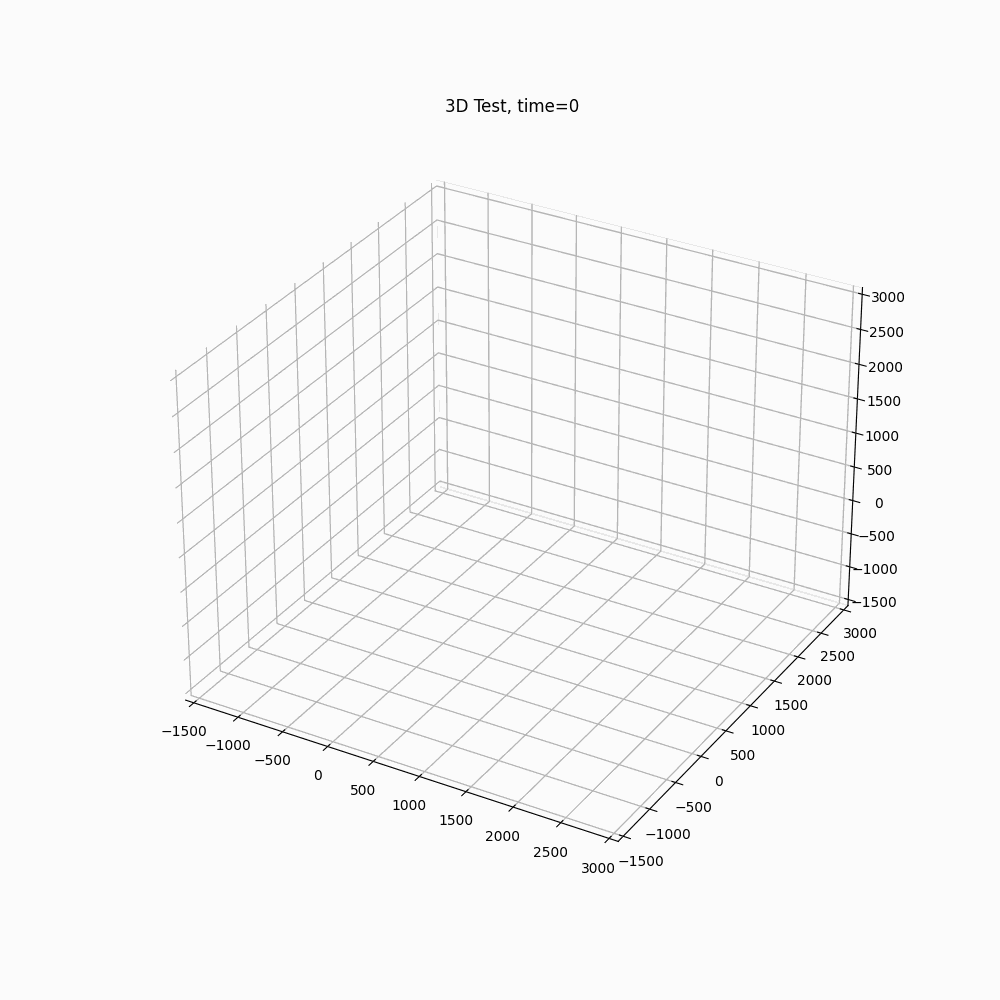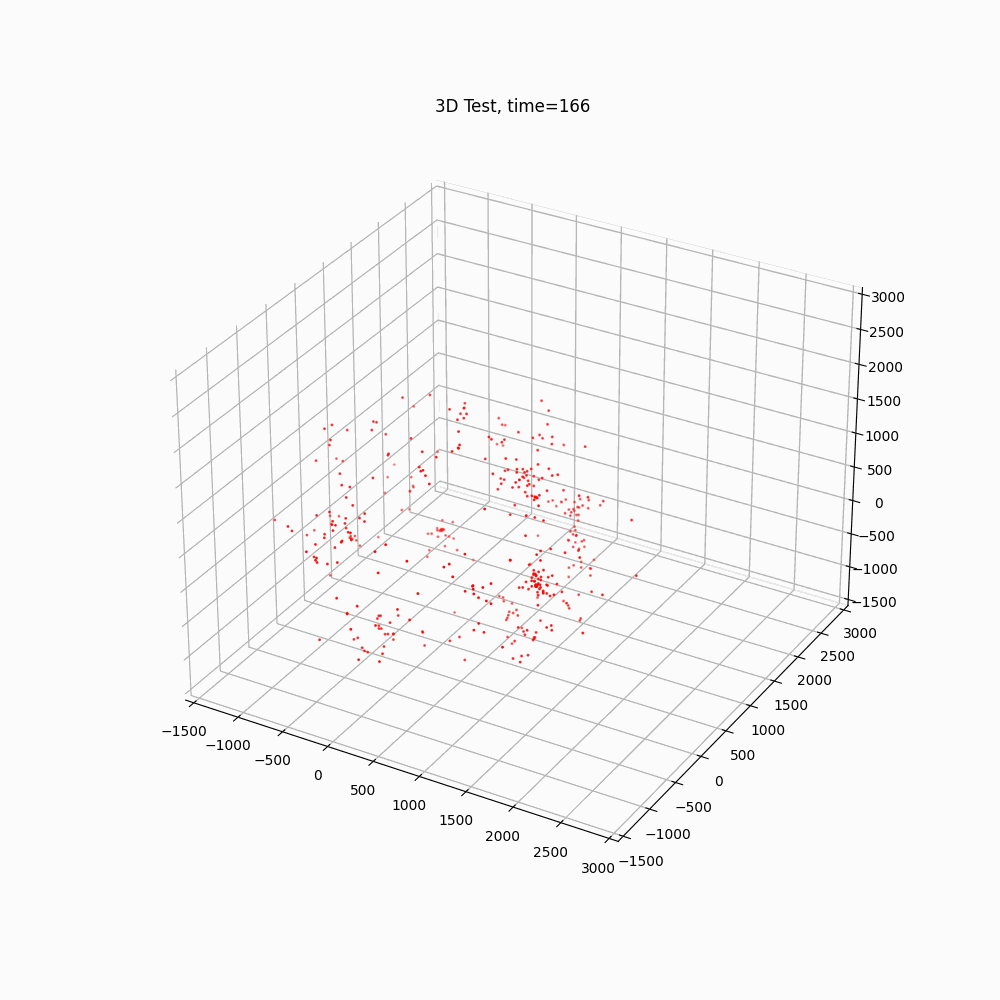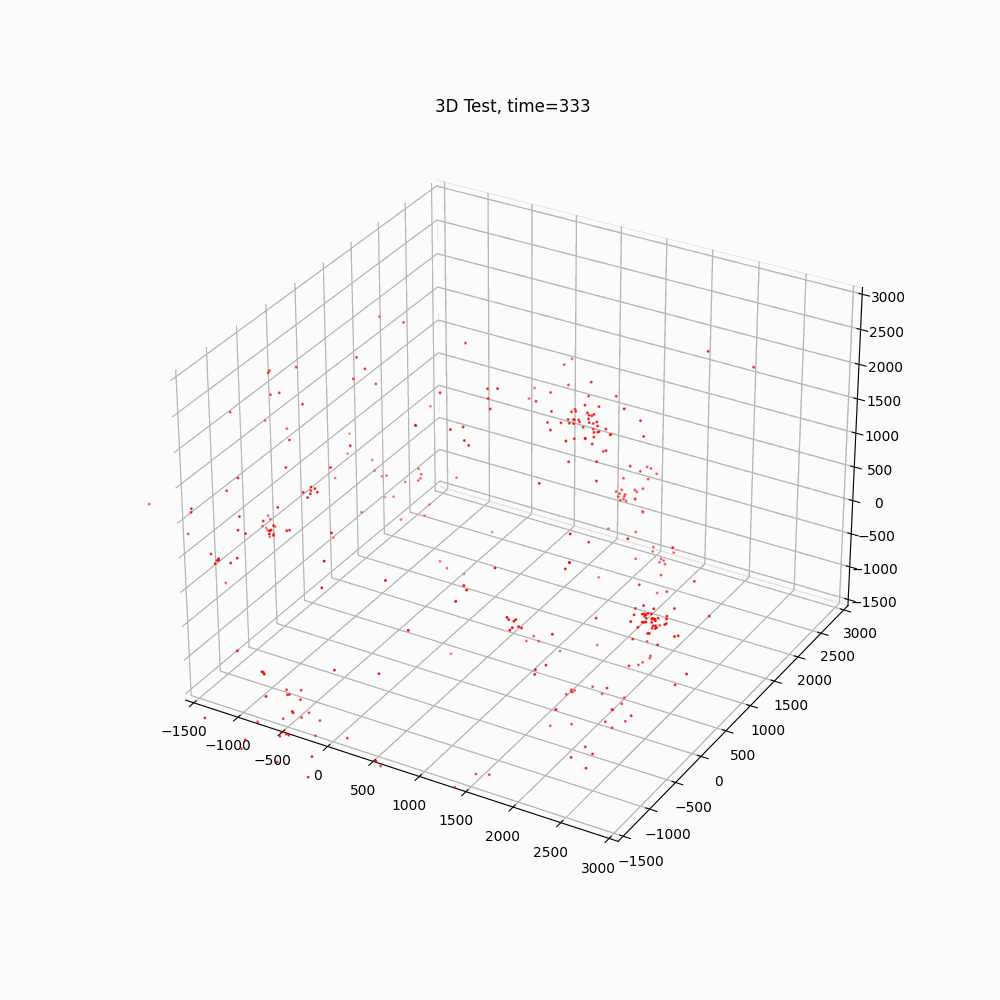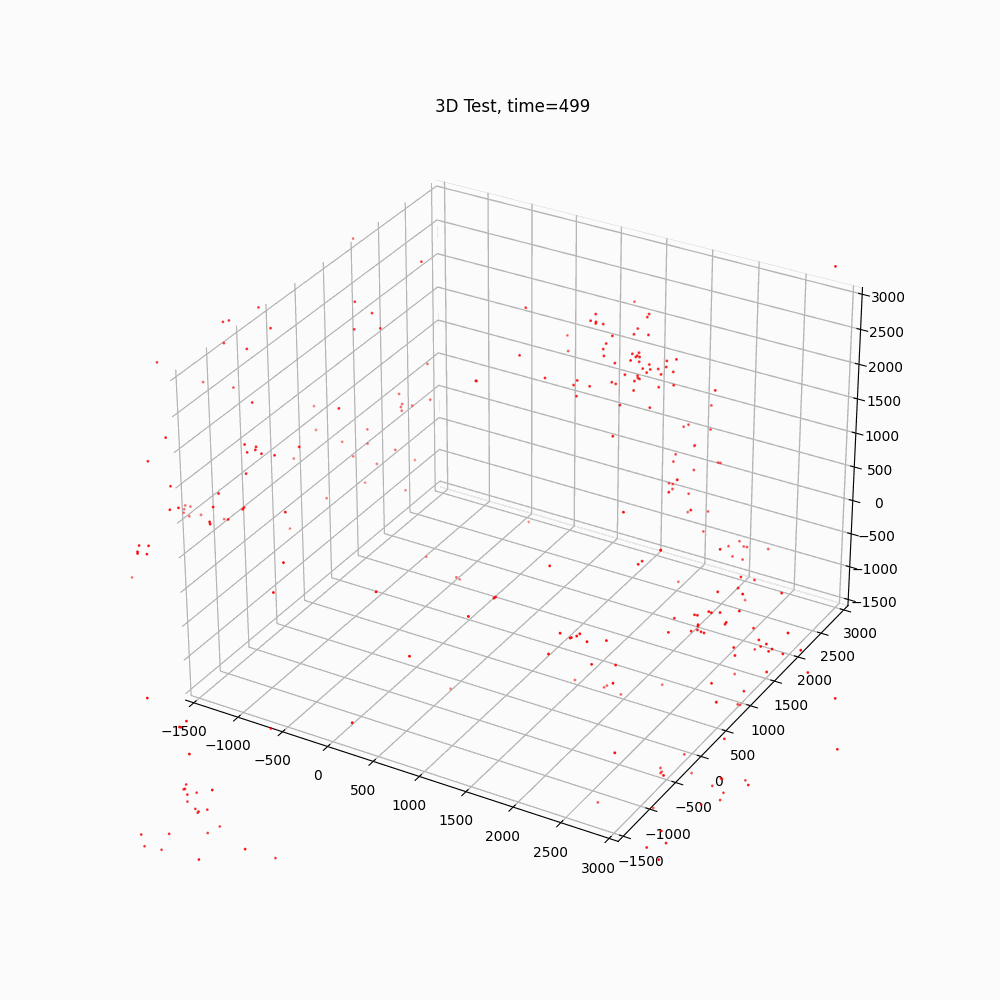
Gravitational Particles
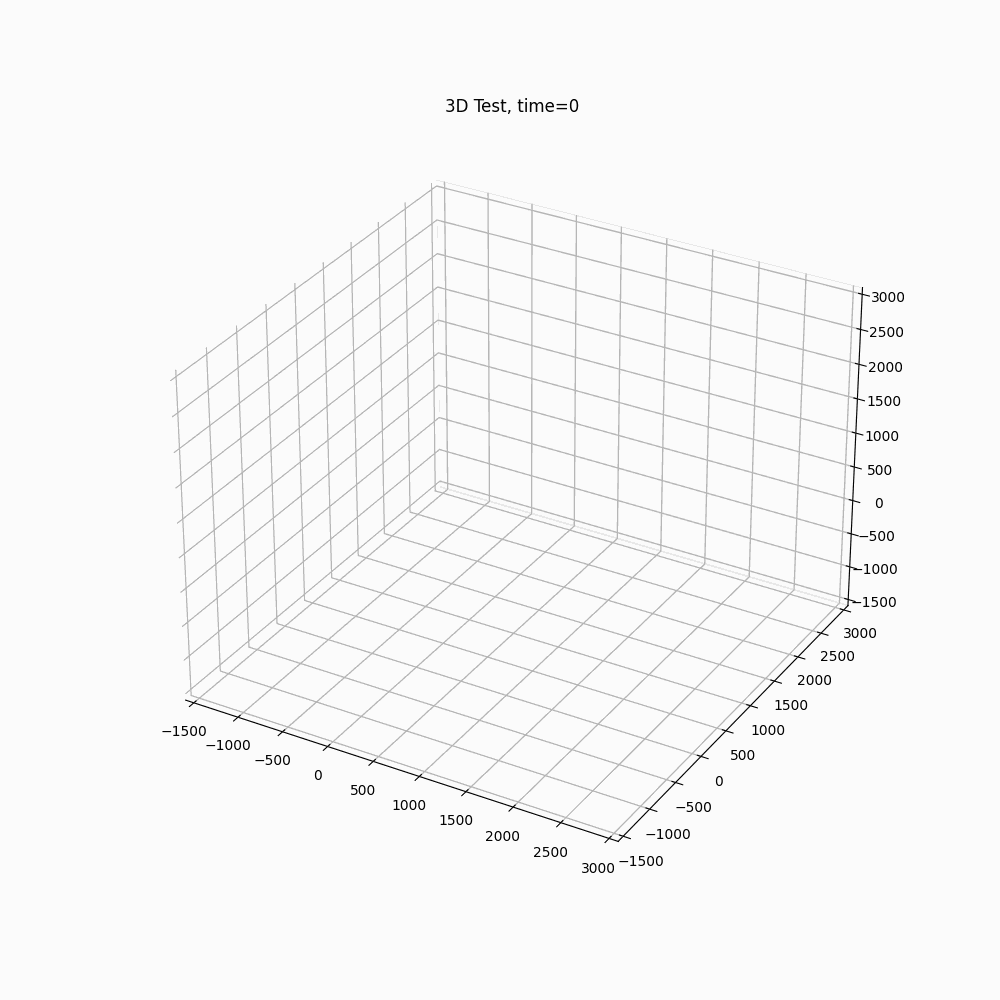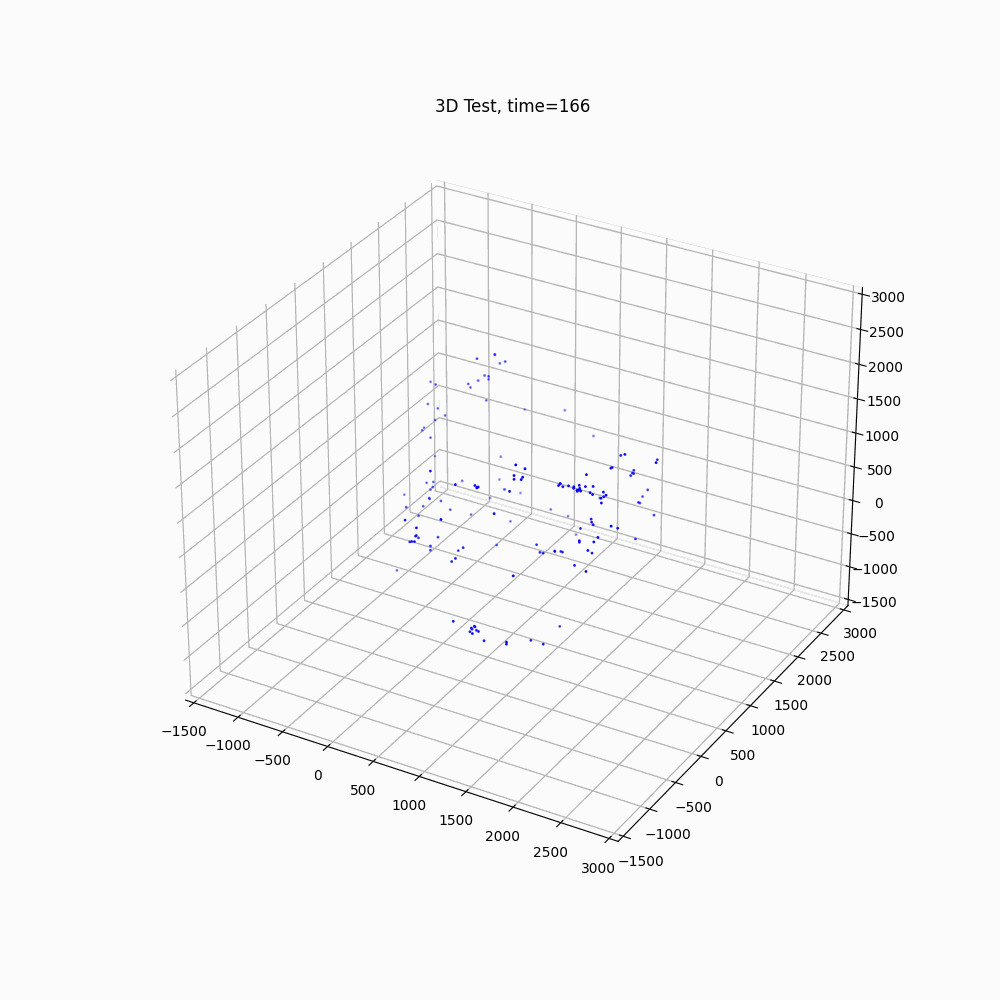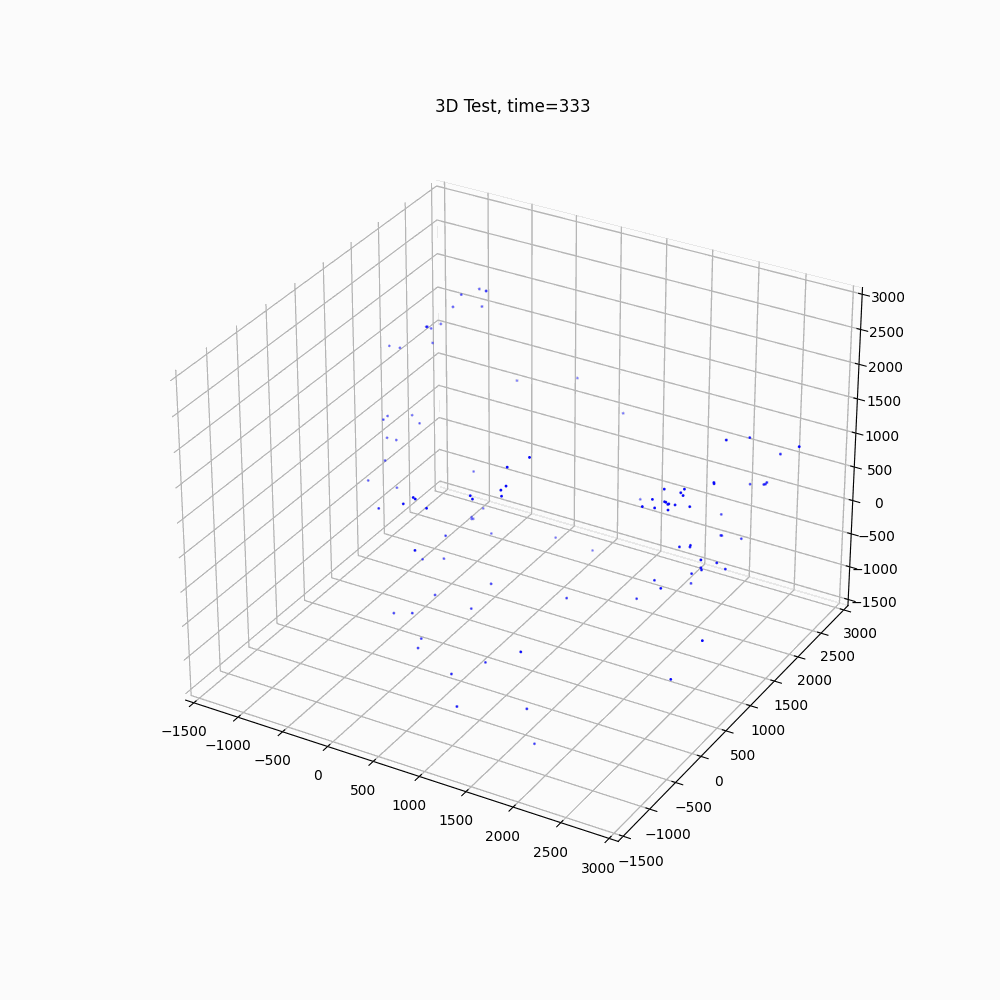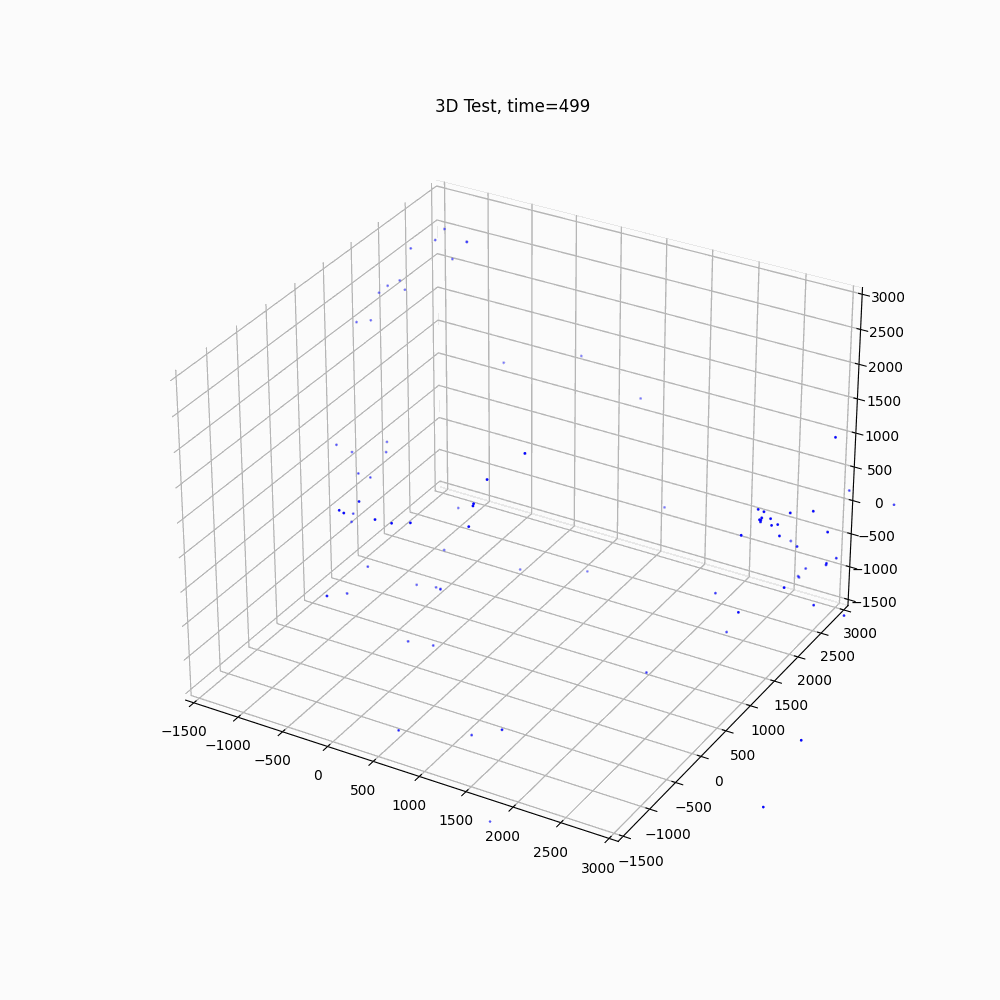
3 Technology Used
The simulation was written in C++ language utilizing Boost library and OpenMPI for multi-processor support. The simulation generates a text file containing the locations of each particle every 1000 iterations. The text file is read via a Python script and creates an animated gif displaying a frame for each step. The full simulation can be viewed online at Saint Claire’s Scientific Research and Development website [3]. A copy of the code may be requested by contacting the author.
Conclusion
In conclusion it has been shown a model based on a non-complex concept of an antigravity particle produces web like filaments between clusters of particles. If an antigravity type of particle existed and was hidden from known observation, by the results of the simulation, it has the potential to help describe webbing filaments in a cosmic setting. These results should not be considered a legitimate explanation of the filaments, but rather an illustration of how a simple concept can often produce unexpected results. Which in turn may inspire new thought and understanding of nature.
References
[1] Bondi, H. (1957) Negative Mass in General Relativity. American Physical Society, Rev. Mod. Phys, 29, 423-428 https://doi.org/10.1103/RevModPhys.29.423
[2] Austin, R W (2017) Gravitational Time Dilation Derived from Special Relativity and Newtonian Gravitational Potential, European Scientific Journal, 13, #3, p 447 https://doi.org/10.19044/esj.2017.v13n3p447