In Einstein’s theory, he required the speed of light to be a universal speed limit. Please remember that nothing can travel faster than the speed of light. Second, concerning the speed of light, every observer would measure the speed of light to be the same, regardless of where they measured it. This may sound obvious, but it isn’t. If a person is traveling in a car at 100 mph and juggles a ball in her hand, the people in the car will observe the ball as not moving forward or backward as it is juggled. The only movement observed in the car is the up-and-down motion of the ball being juggled. But, if an observer is outside the car and stationary relative to the moving car, she will observe the ball moving both up, down, and forward. The forward motion arises from the car moving.
If the person in the car throws the ball from the back seat to the front seat at 10 mph, the people in the car will see the ball travel at 10 mph. The stationary people outside the car will see the ball move at 100 mph (the speed of the car) plus 10 mph (the speed of the tossed ball from the car) for a total of 110 mph. This in everyday life becomes intuitive. But, Einstein postulated if light is emitted from a moving car, the people inside the car and those stationary outside the car will observe the light propagate at the same speed! A postulate that has stood the test of time for over a century. This one postulate produces several “strange” behaviors. Strange in the sense of one’s everyday intuition. For instance, if the people in the car observe the light move for one second, it would travel c meters, where c is the speed of light. The ones outside the car would also see it move c meters. One result of this is the clocks in the moving car “ticked” at a different rate than those clocks outside the car (stationary relative to the car). This means both space and time are dilated or warped because of relative motion. This is part of Einstein’s 1905 paper that founded Special Relativity and was used by his teacher, Minkowski, to develop a metric space. Yet, this did not cover the case of acceleration.
These postulates were transferred to Einstein’s theory of general relativity while addressing acceleration. Consider Einstein’s elevator thought experiment. If the elevator was stationary and a ray of light was transmitted from one side of the elevator to the other side, the ray of light would appear to move in a straight line, see Figure 2.4.
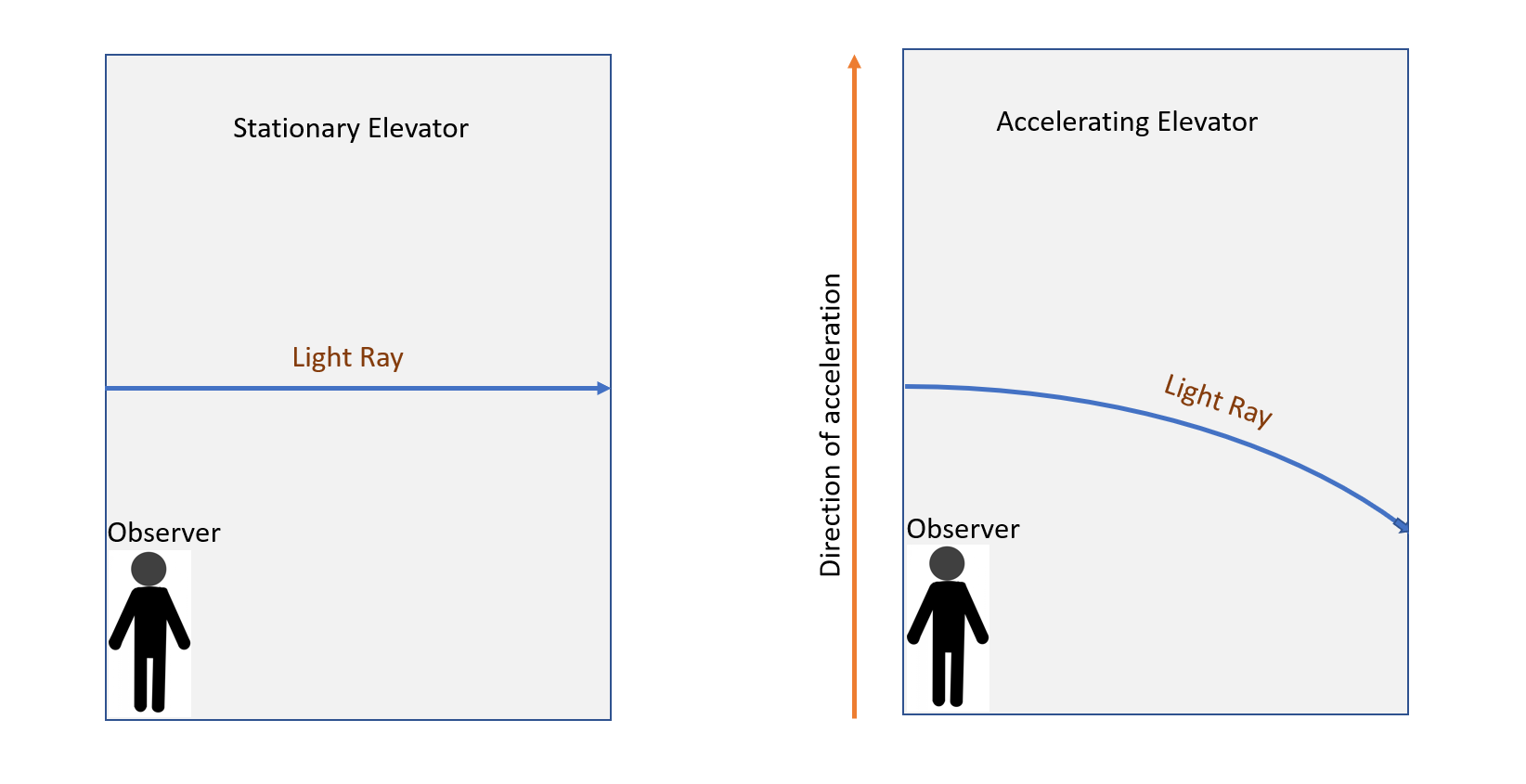
Einstein understood much of the consequences of this and developed a four-dimensional approach. The approach included the three dimensions of freedom we experience in everyday life (height, width, and length, often displayed mathematically as x,y,z coordinates in an Euclidean space) plus time. Rather obvious is the dilemma of how one merges time and space. Time is not space, in the sense that you can multiply time by length and result in an area like that of length multiplied by length. To resolve this issue, Einstein used the postulate that all observers view the speed of light “c” the same. Thus, he set up a coordinate system of x,y,z, and ct. Where ct is the distance a ray of light travels in a unit of time. By doing this, all coordinates (x,y,z,ct) have the same unit. There was one issue, though: ct is restricted by t (time). Why is it restricted? The speed of light is a universal speed limit. If one set out to measure the distance in a 4-dimensional system using the Euclidean distance, they could arrive at a scenario in which light traveled faster than c. To accommodate this, a distance formula was used that subtracted the distance light travels in a unit of time from the Euclidean distance, see Figure 2.5.
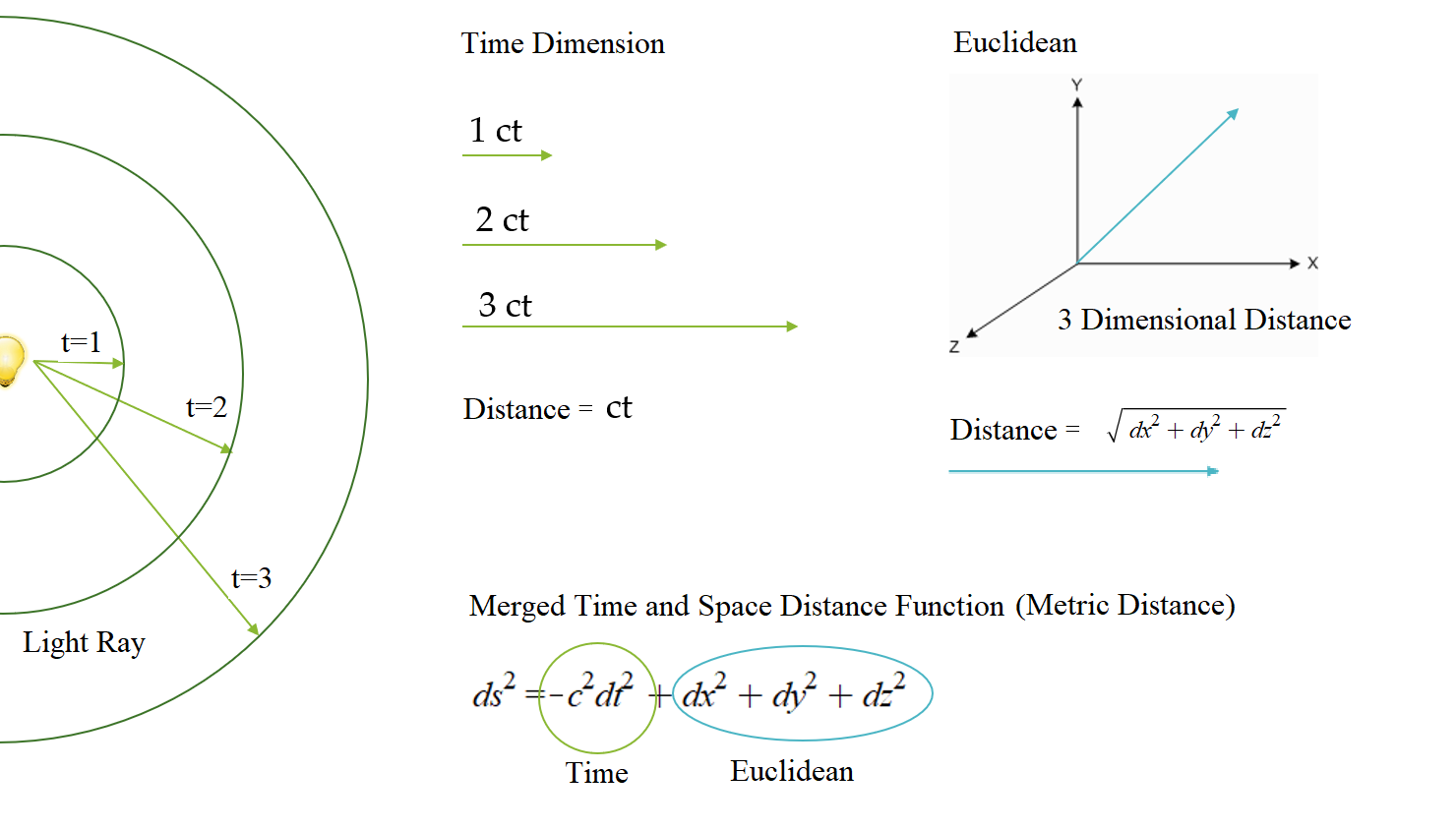
In Figure 2.5, the unit distance for light travel is ct, the x,y,z form the unit (basis) for Euclidean space. The distance in Euclidean space is “calibrated” by the speed of light in this metric. Notice the minus sign in the distance formula in Figure 2.5. If the Euclidean distance is less than the light distance, the distance is negative. If they are equal, the distance is zero. Lastly, if the Euclidean distance is greater than the light distance, the distance is positive. This set three definable sectors within spacetime. If \(c^2t^2>E^2\) where E is the Euclidean distance of x,y,z coordinates then it is called timelike, if they are equal it is call lightlike, and if \(c^2t^2<E^2\) it is called spacelike. In case the reader is wondering, our natural everyday experience falls well into the timelike sector. This is because we cannot move faster than the speed of light, nor (at least that has been discovered) can information travel faster than the speed of light. This cosmic speed limit constrains us to a timelike sector and experience.
This method is ingenious and works rather well. However, when using this method, one does not adhere to a fundamental requirement of Riemannian space. Remember, the metric is determined by the inner product, and the inner product must be positive definitive. This means the metric must never be negative, and it can only be zero when the metric is formulating the distance between a point and itself. This violation was known, and its inclusion was not a mistake. It was given a name (listed earlier), a pseudo-Riemannian metric. This term indicates the metric covering the manifold can have a negative, zero, or positive value. This metric violates the Riemannian geometry structure and, in the author’s experience, is often quickly passed over by physics instructors with hand waving and dashing to the next subject. It is not given rigorous treatment before the students of physics, and since the professor said it, it is often accepted with little questioning.
It is accepted for good reason; it duplicates and predicts what experimental evidence has been discovered in nature. The perihelion shift of Mercury, the curvature of light about the sun, time dilation, black holes, and gravitational waves. With such an impressive list of successes, it appears foolish to question the legitimacy of using a pseudo-metric. Similar to the lack of questioning of Euclidean geometry due to its effectiveness. Only when concerns arose about measuring large areas of the surface of the Earth was it questioned. So, is there a place of concern about using a pseudometric in General Relativity? Possibly. Considering the event horizon of a black hole, it is commonly accepted that any information (or particle) inside this mathematical boundary can never reach the outside of that boundary. This leaves an area in physics (and math) that is a complete mystery. The mystery is multi-faceted because current understanding doesn’t know if the mystery is a physical mystery or a mathematical artifact not relevant to reality. In other words, is it possible to understand if the mystery arises from the choice of a pseudo metric causing science to look for something that is purely mathematically induced? Or does it represent something within nature? The event horizon comes from a trajectory on the manifold when it crosses from a time-like area to a light-like area. The light-like area is the event horizon. What is beyond the event horizon? That, to is a mystery. Does it even exist in reality?
This one application of a pseudo metric may give mathematical artifacts that provide other violations of Riemannian geometry. As will be discussed and shown later in this book, the choice of a pseudo metric in certain scenarios may produce a discreteness to the metric. In other words, the metric has a minimum distance and cannot be reduced to an infinitesimal point. This violates Riemannian geometry requirements that the manifold be smooth. The author feels the quick embrace of Riemannian Geometry by Einstein, along with possibly having a mono-focus on Riemannian geometry led to a very robust theory that gave incredible results and continues to this day (just consider gravitational waves). However, this leaves within the success of the theory a potentially buried landmine. The success of the theory came by violating the requirements of the math of Riemannian geometry. Thus, as engineers of the theory, they reduced the integrity of a component used in the structure. Many of the areas that remain a mystery to scientists in General Relativity occur in the areas of the violation of Riemann’s rules, like the black hole event horizon. Is it possible because of the success of the theory these landmines are now disguised as mysteries? What if Gauss, in measuring the Kingdom of Hanover, would have said Euclid is correct, and there remains a mystery in the Kingdom of Hanover? A physical mystery that bends the space and causes the angles of a triangle not to equal 180 degrees? Gauss could argue it happens nowhere else except in these sizeable areas. This idea seems preposterous in modern retrospect, but if Gauss would have embraced Euclid’s geometry as the “law”, it would be easy to see how the world would have arrived at a mystery in Hanover. Is the mysteries of General Relativity the same type of mystery? Do they arise from the manipulation of the math (the metric) that creates an event horizon? Could the black hole be our modern mystery in Hanover? They happen only in the very condensed area of our maps, much like Euclid’s problems, which only occur in the mapping of large areas.
Einstein’s GR was based on the equivalence principle, which states that acceleration and gravitational potential acceleration are identical. His field equations in GR change the metric of a local space because of the influence of energy, such as acceleration. This is done mathematically by a stress-energy tensor. By changing the metric, it curves all space around the energy, thus propagating the change across the manifold. Yet an accelerating object such as a rocket does not propagate a curvature across the manifold even though it experiences time dilation because of acceleration. In other words, a clock tethered to a string and twirling it is being accelerated about a circle. This tethered clock will experience a time dilation relative to a non-accelerating clock. Yet a stationary clock immediately beside the path of the circling clock will not experience a dilation because of the passing clock on the string. The accelerating clock on the string does not propagate a change in the metric across the manifold. It appears only to be local. This seems in contradiction to Einstein’s equivalence principle since a mass in space produces acceleration that propagates across the manifold according to the metric. Yet another mystery of GR and our current understanding. It is also a limitation of the Riemannian metric. The metric does not have a mathematical way of representing a local effect that doesn’t propagate (or affect) to areas around it.
Between 1900 and 1915, another revolution took place in science. The work of Max Planck showed a solution to the ultraviolet catastrophe could be given if energy was exchanged in discrete amounts. Einstein was aware of this development and showed that his photoelectric effect agreed with Planck’s constant (one of Einstein’s 1905 papers). A paper that won Einstein the Nobel Prize in 1921 [30]. There remains a mystery as to why Einstein embraced Planck’s work, which contained discreteness and required a non-continuous mathematical solution, while in General Relativity, he embraced a classical field theory that is continuous. Is it possible in Einstein’s desperation to find the math to correspond with his theory, he overlooked or took shortcuts that, if properly constructed, may have pulled two grand theories together instead of apart? This question will be investigated, and a mathematical approach will be formulated to tackle his theory without using Riemannian geometry. In the honor of Einstein, a thought experiment will be put to the test, and its consequences will be evaluated. Shall we start?