Around 300 BC, a Greek mathematician named Euclid wrote a book titled The Elements . Historically, it was a first of its kind. Euclid started with a simple concept and built new concepts from the previous concepts. Each grew in complexity as its formation depended on the formation of prior postulates and propositions. From this work arose the modern teachings of Euclidean geometry. Concepts that canonized today’s elementary teachings were developed, such as the sum of triangle angles equaling 180 degrees. The derivation of the law of cosines and, eventually, trigonometry naturally grew from the postulates of Euclid’s work.
Relevant teachings from Euclid concerning this work include his writings on lines, parallel lines, and planes. In Euclidean geometry, the connection of two points by their most direct, shortest path is called a line segment. Functionally, these line segments are part of a line extending infinitely in each direction beyond the two points. Euclidean geometry has only one path, which forms the shortest distance between two points. From the concept of a line, one may form a new proposition that two lines can be created in a manner they will never cross. These two lines are termed parallel lines. As they traverse infinity, they will never cross each other.
By taking two lines that intersect (thus, they are not parallel), it is possible to form a plane. A plane is a flat surface that both lines are “bound” to. They will remain on the plane infinitely.
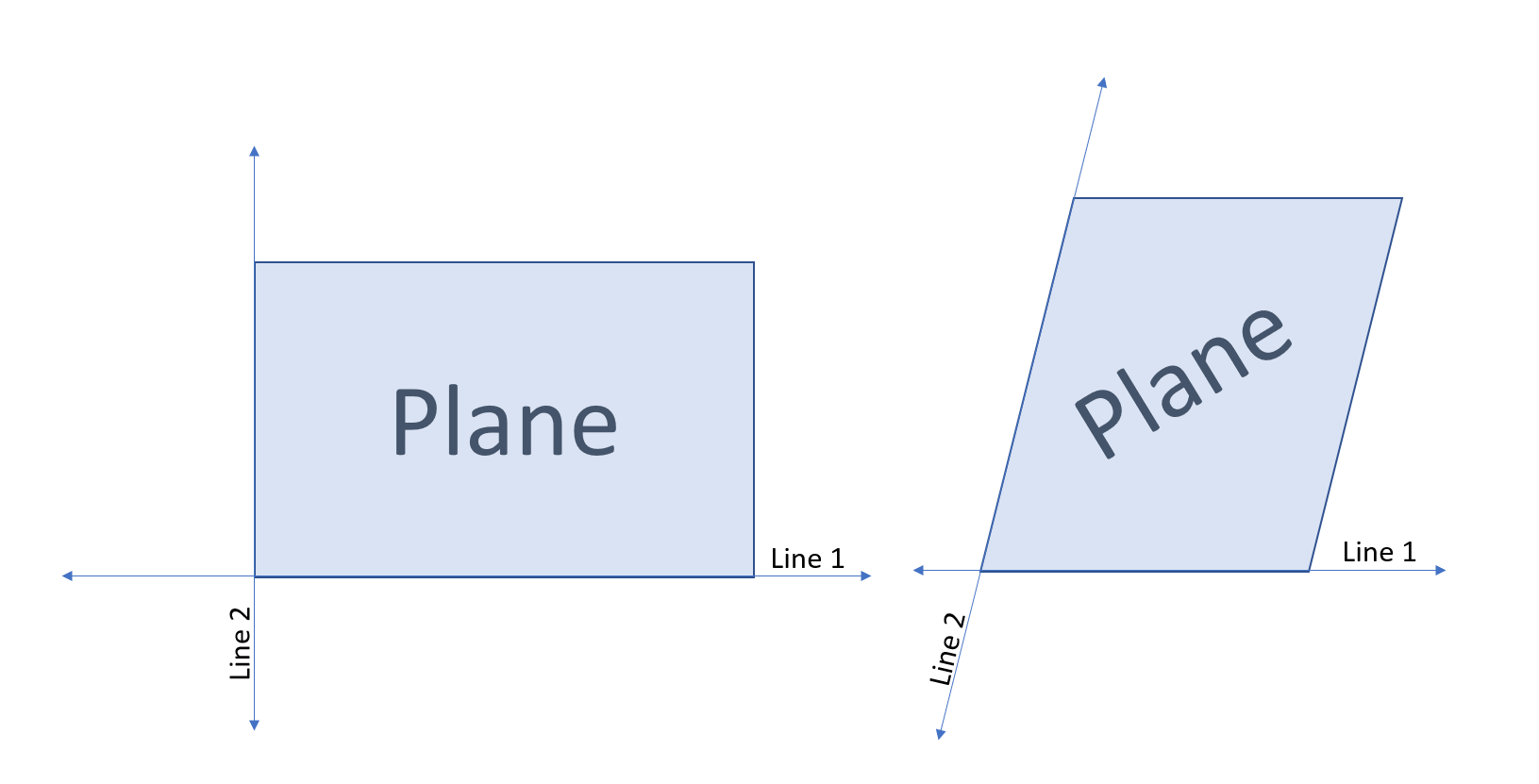
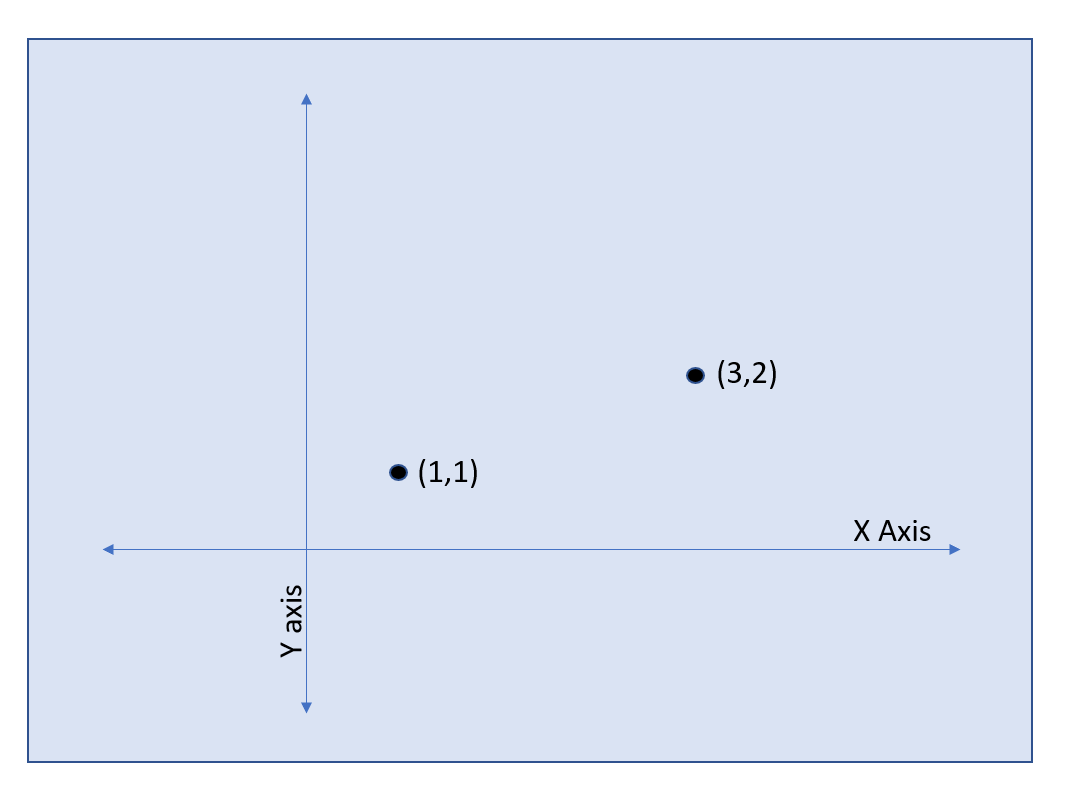
It is possible with these two non-parallel lines to “map” the plane (an infinite “flat” area) they form; see Figure 2.1. This is most commonly known in modern algebra as a two-dimensional plane with x and y coordinates applied to every location (point) on the plane; see Figure 2.2.
Once the plane has been mapped, new functions can be derived, like the distance between two points, comparing a value over time (charting), or more profound concepts like derivatives and anti-derivatives (aka calculus). Even the intersection of two planes (like the intersection of two non-parallel lines) allowed humans to map three-dimensional space, an achievement mimicking humans’ everyday experience.
The level of impact Euclid’s building precept upon precept had on math and later science cannot be overemphasized. His methods are still in use today and are praised by scholars millennia later. Euclid provided a way for a person anywhere to apply his logic and arrive at the same conclusion or result as anyone else would. A student located in the far reaches of the world, away from a different student, will be able to draw a triangle on a flat surface and measure the interior angles. Both students will conclude that the sum of the angles is 180 degrees, regardless of where they are in the world. This was a brilliant turning point in the logic of humankind. It was so clever it lasted thousands of years, with little or no question of its accuracy.
Historically, there were times when some of Euclid’s postulates were challenged. Still, they remained intact and unquestioned until a notable mathematician named Carl Friedrich Gauss (1777-1855) was given charge of surveying land for the Kingdom of Hanover. It was here that the teachings of Euclid began having issues (or cracks) within its logic, as it needed to match the observations and measurements on a large scale over the surface of the Earth. Later, Gauss, as a teacher, had a student named Georg Friedrich Bernhard Riemann. Riemann formally advanced Euclidean Geometry into a new realm, today termed Riemannian Geometry.