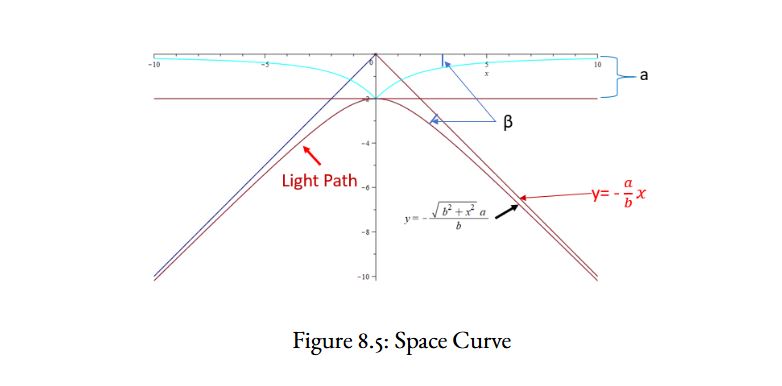
In NUVO theory, light does not experience a local effect (due to acceleration). Thus, its trajectory only reflects the global effect of a massive body on space. As such, one may assume the curvature of space can be measured by the trajectory of a photon. It has been shown that NUVO predicts a photon will follow a hyperbolic path about a massive object.
The hyperbolic light path with asymptotic lines was shown. In addition, a cyan-colored line is drawn, representing the departure from flat space along the x-axis. At each location along the x-axis, a length (\(\beta\)) is calculated as the distance from the x-axis. This is the path of a light ray when the axis is rotated to represent the asymptotic line. \(\beta\)’s value is determined by subtracting the hyperbolic curve:
\begin{equation}
y = -\frac{\sqrt{b^2+x^2} a}{b}
\end{equation}
from the asymptotic line
\begin{equation}
y=-\frac{a}{b}x
\end{equation}
The maximum value for \(\beta\) is \(a\) when the \(x\) value is zero distance from the center of mass. Away from the \(x\) zero distance, \(\beta\)’s value is dependent on distance from the center of mass and reduces proportionally to the distance. The equation for \(\beta\) is:
\begin{equation}
\beta = -\frac{a \left(\sqrt{(r+a)^2 + x^2}-x \right)}{r+a}
\end{equation}
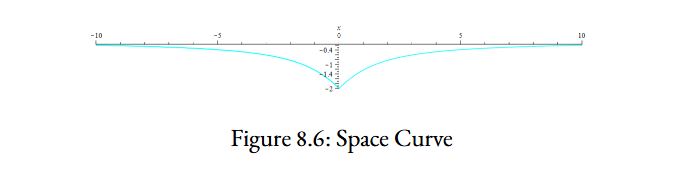
Consider where the cyan-colored curve is isolated. In a scenario where the center of mass is oscillating, \(\beta\)’s value at a distance \(r\) from the center of mass will oscillate in relation to the oscillating center of mass. This will form a wave that affects space-time at all locations, with the strongest effect near the oscillating massive body.
Using Python with two equal masses rotating about each other, one can simulate the waves emitted that propagate through space and time. This is shown in below.
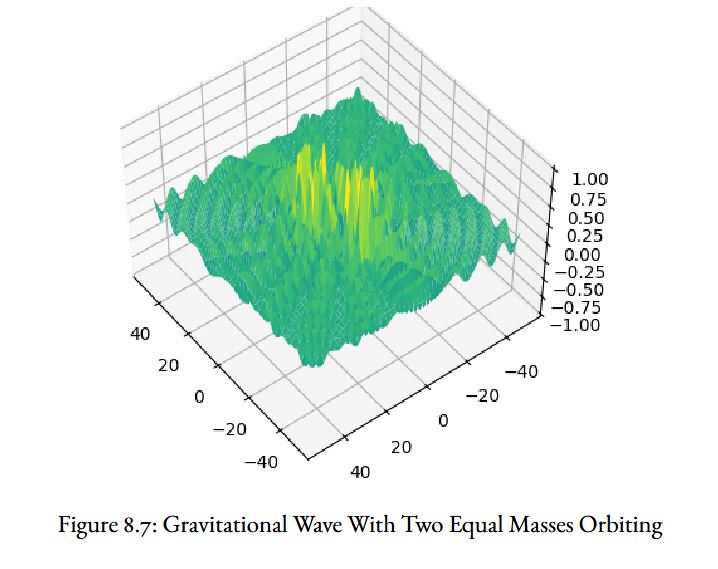
These waves are equivalent in structure to General Relativity’s gravitational wave. As they travel past a location in space, they affect time and space. Because these waves affect time and space, they also affect the observation of measurements, such as the energy of a photon.