Light, behaving like a particle with its interaction with matter, and behaving like a wave in its propagation through space, has the ability to carry different energy levels depending upon its wavelength or frequency. In NUVO different locations in space may (and most likely will) have different sinertia levels. Thus, if a photon passes through a volume of space, its observable energy depends on the local space. This is unlike mass which maintains an invariant rest energy magnitude. NUVO also embraces the concept that light, when created, takes on the characteristics of the local space it was created in and maintains this characteristic until it is annihilated. During the “lifetime” of a photon, it will traverse space with different sinertia levels and be observed at different energy levels. A method by which to observe this energy variation is by measuring the photon’s wavelength \(\lambda\) from creation to annihilation.
Via NUVO, if \(\lambda_{emit}\) is the wavelength of an emitted photon and \(\lambda_{obs}\) is the wavelength of the photon observed at a different location, then
\begin{equation}
\Phi_{emit} \lambda_{emit}=\Phi_{obs} \lambda_{obs} = \lambda_{\mathcal{E}}
\end{equation}
where \(\lambda_{\mathcal{E}}\) is the wavelength of the emitted photon as observed in Exemplar space.
In examining the shift in wavelength, the value \(z\) is defined as
\begin{equation}
z=\frac{\lambda_{obs} – \lambda_{emit}}{\lambda_{emit}}
\end{equation}
and
\begin{equation}
1 + z = \frac{\lambda_{obs}}{\lambda_{emit}}
\end{equation}
Thus, in NUVO terms, 1 + \(z\) is
\begin{equation} \label{eqZValue}
1+z=1 +\frac{\Phi_{emit}-\Phi_{obs}}{\Phi_{obs}} = \frac{\Phi_{emit}}{\Phi_{obs}}
\end{equation}
Note that this initially looks the opposite of the \(z\) value as obs – emit is in the numerator of the canonical expression, and emit-obs is in the numerator of NUVO. This arises from transforming all values to Exemplar space and making the comparison there. Thus,
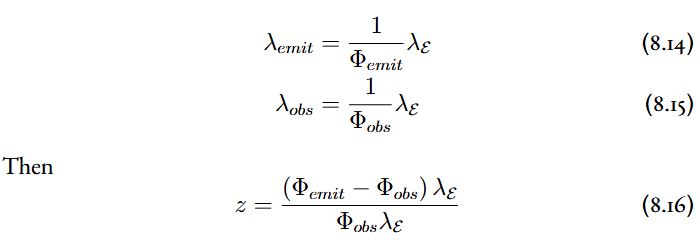
Arriving at the NUVO value of 1 + z in evaluating the red or blue shift of a photon’s wavelength. Lastly, note because this is an instantaneous (or static) measurement, the static transformation is applied for \(\Phi\).
When the observer is in Exemplar space, and the emission of the photon is from Privo space, there will always be a redshift as \(\Phi_{obs} = 1\) and \(\Phi_{emit} > 1\). Correspondingly there is a blueshift when the light is emitted from Exemplar space and observed in Privo space. In General Relativity terms, this is the equivalent of saying there is a gravitational redshift of light when traveling from inside the gravity well to outside the gravity well, and there is a blueshift of light when traveling from outside the gravity well to inside the gravity well.