According to NUVO theory, massless particles do not have a local effect. They do not have pinertia. Without pinertia, there is no reduction in space’s sinertia, thus no propagation of any effect of their presence in space. Massless particles can interact with mass, a process discussed in detail in Volume 2. Without pinertia interaction, a massless particle is much like the elementary physics lesson where a frictionless surface is introduced. Massless particles move through space without friction. They do not interact with space in a way that causes a change in sinertia.
The commonly accepted logic is a ray of light will bend toward a massive object. In Newton’s paradigm, gravity acts as a force and draws it into the massive object. The previous chapters showed that with the NUVO transformation, any orbit of a system that has added length causes a shift in the observational number line. One interpretation of this added space-time is that mass expands space about it proportionally to its magnitude. This is in contrast to normal logic.
Consider a ray of light traveling left to right as represented by the red line in the figure below. The top path represents the light ray when there is no expansion in space, and the light follows a “straight” path from left to right. But, if the mass caused an expansion in space, the light ray would be “pushed” upward depending on the amount of expansion caused by the mass. This may be visualized in the other light rays shown in the figure below. As the expansion grows in volume of space, the curve becomes more pronounced.
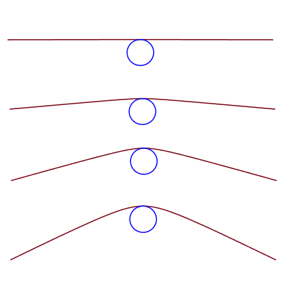
With this in mind, consider the trajectory a light ray would take about a massive object based on the NUVO transformation. The NUVO transformation in dealing with light only has a potential effect, not a kinetic effect. It covers both space and time. Therefore, the transformation takes the form of
\begin{equation} \label{eqMasslessTransform}
\phi = 1 + \frac{2 G M}{r c^2}
\end{equation}
Graphing grid lines with both Exemplar space and privo space about a mass, the privo lines become hyperbolic instead of straight lines, mimicking the figure above. The figure below graphs these lines, with the straight grids being Exemplar space and the curved grid being the transformed grids from exemplar space to privo space (using the equation for the massless transformation for the transformation). Exemplar space uses a Euclidean metric, and privo space has the transformed Euclidean metric for each point in space. A metric derived from this transformation can be found in the appendix.
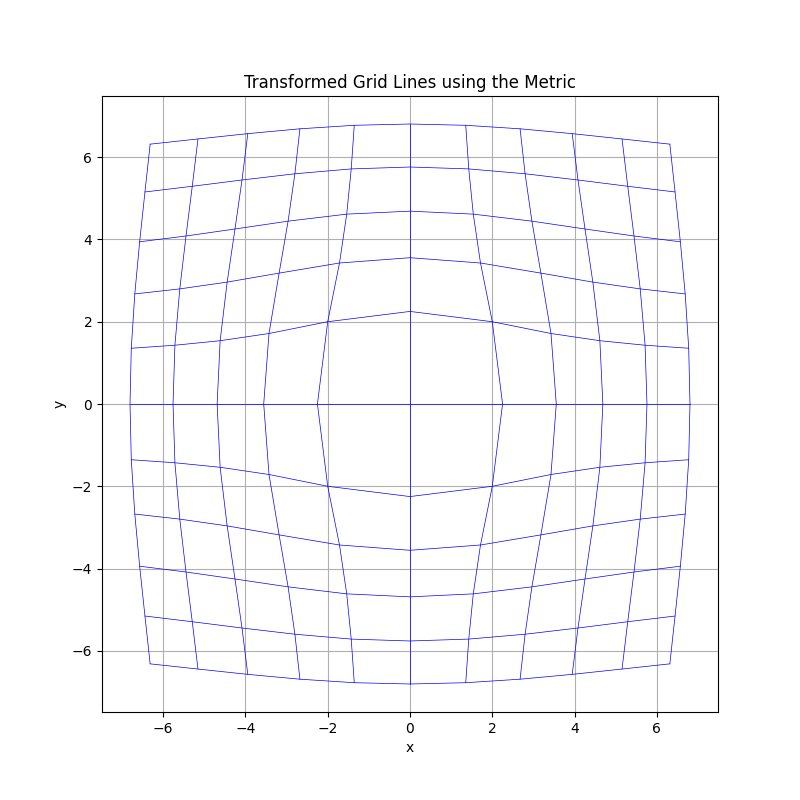
The figure above shows a two-dimensional example of the space (not the local effect of a particle moving in the space) about a massive object. Since there are no local effects and light has no local effect, this graphing is an illustration of the paths light would take in the space surrounding a massive object. The following section discusses this concept and applies a mathematical approach to understanding the NUVO transformation and light trajectories.