Circular Orbit
A particle under the influence of a gravitational field will have an instantaneous velocity of
\begin{equation}
v=\sqrt{\frac{2 G M}{r}}
\end{equation}
and an advance of
\begin{equation} \label{eqCircularAdvance1}
2 \pi A r_{\mathcal{E}} = 2 \pi \left( 1 + \frac{v^2}{2 c^2} + \frac{2 G M}{r c^2} \right) r = 2 \pi r+\frac{6 \pi G M}{c^2}
\end{equation}
Thus there is an invariant advance for all circular orbits in the system of
\begin{equation} \label{CircularConstantAdv}
adv=\frac{6 \pi G M}{c^2}
\end{equation}
For the advance in radians, divide by the radial distance of the orbit.
\begin{equation} \label{CircularConstantAdv2}
adv_{radians}=\frac{6 \pi G M}{r \: c^2}
\end{equation}
Elliptical Orbit
In an orbit that is elliptical, one can place a dependency of $r$ to $\theta$. In this scenario, there is a constant advance for all orbits. Consider $r$ defined as
\begin{equation}\label{eqRinTheta}
r = \frac{a(1-e^2)}{1 + e \: cos(\theta)}
\end{equation}
Then the orbital equation becomes:
\begin{equation} \label{eqAdvance}
\frac{6 \pi G M}{a \left(1-\mathit{ec}^{2}\right) c^{2}}
\end{equation}
This is exactly what General Relativity predicts as the advance of an orbiting planet, such as mercury \cite{Misner-Gravitation}. Thus, another way to calculate the advance is to integrate over the circumference of the orbit to obtain an accurate value of the advance. This looks like:
\begin{equation}
\int_{0}^{1}\int_{0}^{2\pi}\left( 1 +\frac{3 G \cdot M}{\left(\frac{a \cdot (1-.\mathrm{e}^{2})}{1+\mathrm{e}\cdot \cos (\theta)}\right)\cdot c^{2}}\right) d \theta dP
\end{equation}
Another method to calculate an approximation using the constant length of and advance is compared. One calculates the perimeter of the elliptical orbit. A good approximation is to use:
\begin{equation}
p=4 a \int_{0}^{\frac{\pi}{2}} \left(1-e^2sin^2\theta \right)^{\frac{1}{2}} d \theta
\end{equation}
Then take the constant length advance and divide it by the perimeter. Thus, the third approximation is:
\begin{equation}
\text{adv} = \left(\frac{\left(\frac{6 \pi G M}{c^2}\right)}{p}\right) 2 \pi
\end{equation}
The \(2 \pi\) is to obtain the advance in radians. The value for each of these when applied to mercury is:
\begin{equation} \text{adv}_{1} = 5.02 \cdot 10^{-7}
\end{equation}
\begin{equation} \text{adv}_{2} = 5.02 \cdot 10^{-7}
\end{equation}
\begin{equation} \text{adv}_{3} = 4.86 \cdot 10^{-7}
\end{equation}
Subscript 1 is for the constant (non-r-dependent) calculation, subscript 2 is for the integration method, and subscript 3 is for the constant length advance ratio to the ellipse’s perimeter. Note the last one is a very crude estimation, yet nonetheless, it is a close approximation. Using the value \(5.02e-7\) and adjusted out to Earth years, one arrives at a Mercury perihelion advance of \(42.98\) arc seconds per century. This advance matches well with empirical data.
Orbital Decay
This section applies the rule of starting in exemplar space with Newtonian methods. This allows one to follow the steps of applying NUVO and allows the privilege of using established Newtonian methods. Such as the two-body system and the center of mass. This section highlights the following points and illustrates the consequences of each.
- Forces are not equal between two orbiting objects unless they are exactly equal masses and orbiting at exactly equal velocities.
- The difference in forces causes a movement of the center of mass
- The unequal forces cause the smaller mass’s orbit to decay from a stable orbit.
- The movement in the center of mass causes a change in the “number line shift” previously shown.
- The change in the number line shift generates a wave of space-time dilation (paving a path toward gravitational waves)
Force transforms as \(\phi^{-1}\). This transformation implies Newton’s law of equal force with opposite magnitude is not predicted by NUVO. For instance, the gravitational force of the Earth on the Sun is not equal to the force of the Sun on the Earth. As such, the mass with the lesser magnitude will have a greater force upon it than the larger mass. This causes a decay in the orbit of the system. Two masses M and m, with m having less magnitude of mass than M, will have the following forces:
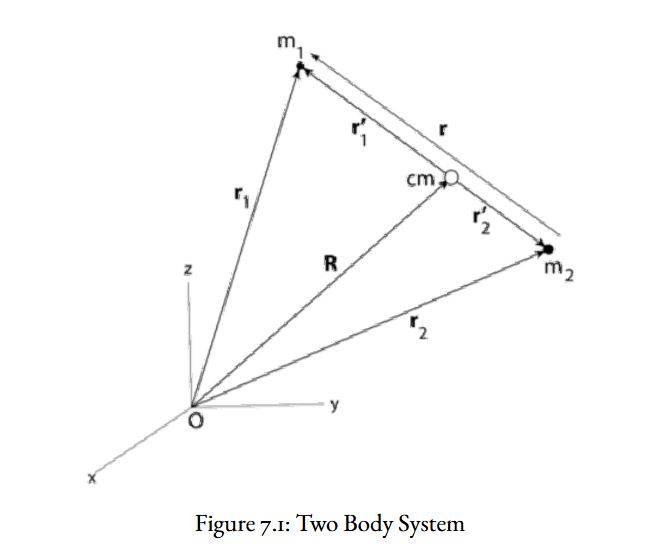

In applying the NUVO transformation, a consequence is two unequal forces are acting on the center of mass.

The difference between forces of \(m_1\) on \(m_2\) and \(m_2\) on \(m_1\) is no longer zero. It is
\begin{equation}
\begin{split}
\mathbf{F} &=\left[\left(-\frac{4G \left(m_{1}-m_{2}\right)}{|\mathbf{r}| \,c^{2}}\right)\cdot \left(\frac{G\cdot m_{1}\cdot m_{2}}{|\mathbf{r}|^{2}}\right)\right] \hat{r} \
&=-\left(\frac{4 G^2 \left(m_{1}-m_{2}\right) m_{1} m_{2}}{|\mathbf{r}|^{3} c^{2}}\right)\hat{r}
\end{split}
\end{equation}
This is in the direction of the larger mass as determined by \(\mathbf{r} =\mathbf{r’_1}-\mathbf{r’_2}\). This indicates the classical center of mass is not stationary or moving with a constant velocity once the NUVO transformation is applied. Instead, it will move with acceleration toward the larger mass, causing a measurable orbital decay.
The change in Newton’s third law by applying the NUVO transformation should not be thought of as two masses having a different force applied (for example, the force by the Earth on the sun does not equal the force of the sun on the Earth). Instead, it should be thought of as the effect of the sun on the local space of the Earth differs from the Earth’s effect on the local space of the sun. Consider two balls moving up and down on the surface of the water. They will each form a wave that travels to the other ball. The effect of each ball on the other ball depends on the displacement of water by each ball, not how each ball is causing a force on the other ball. The balls’ effective force on each other depends on the media (water) and how it propagates the change to each ball. NUVO predicts the same type of scenario for mass in space. One mass displaces much more space than the other mass and, therefore, has a greater “force” applied to the other mass. Without the medium of space to propagate the change, there would be no interaction between the two masses. With this type of analogy, it is logically straightforward to understand how Newton’s third law would not apply.
Before closing out the cosmic orbit section, it is important to note that in calculating the advance, there is a local and a global effect. The acceleration of the satellite causes a local change in available sinertia, and there is an increase in the availability locally. This increase causes a change in the inertia of the satellite and the clocks moving with it. This, in turn, causes the satellite to traverse a greater distance than a classical orbit. The system and orbits of the system (as in our solar system) have a constant advance (when in a circular orbit) because the orbits are determined by the same central mass. If the planets or a satellite were to increase their acceleration via an outside force (other than gravity), the acceleration would alter the constant advance of the system. Because of the global field effect of the central mass, the orbit would be altered unless there was a rigid body system that held the planet in orbit. Like a ball on a string, the same radial distance can be maintained by the ball (from the center of the rotation) regardless of its acceleration.